Using NN’s for Long-Range Forecasts: Electricity Data¶
In this example we’ll show how to handle complex series. The domain here is electricity-usage data (using a dataset from the UCI Machine Learning Data Repository), and it’s a great example of a challenge for traditional forecasting applications. In these traditional approaches, we divide our model into siloed processes that each contribute to separate behaviors of the time-series. For example:
Hour-in-day effects
Day-in-week effects
Season-in-year effects
Weather effects
However, with electricity data, it’s limiting to model these separately, because these effects all interact: the impact of hour-in-day depends on the day-of-week, the impact of the day-of-week depends on the season of the year, etc.
[2]:
BASE_DIR = 'electricity'
SPLIT_DT = np.datetime64('2013-06-01')
DEVICE = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
Data-Prep¶
Our dataset consists of hourly kW readings for multiple buildings:
[4]:
df_elec.head()
[4]:
| group | time | kW | dataset | |
|---|---|---|---|---|
| 0 | MT_001 | 2012-01-01 00:00:00 | 3.172589 | train |
| 1 | MT_001 | 2012-01-01 01:00:00 | 4.124365 | train |
| 2 | MT_001 | 2012-01-01 02:00:00 | 4.758883 | train |
| 3 | MT_001 | 2012-01-01 03:00:00 | 4.441624 | train |
| 4 | MT_001 | 2012-01-01 04:00:00 | 4.758883 | train |
Let’s pick an example group to focus on, for demonstrative purposes:
[5]:
example_group = 'MT_358'
[6]:
df_elec.query(f"group=='{example_group}'").plot('time', 'kW', figsize=(20, 5))
[6]:
<Axes: xlabel='time'>
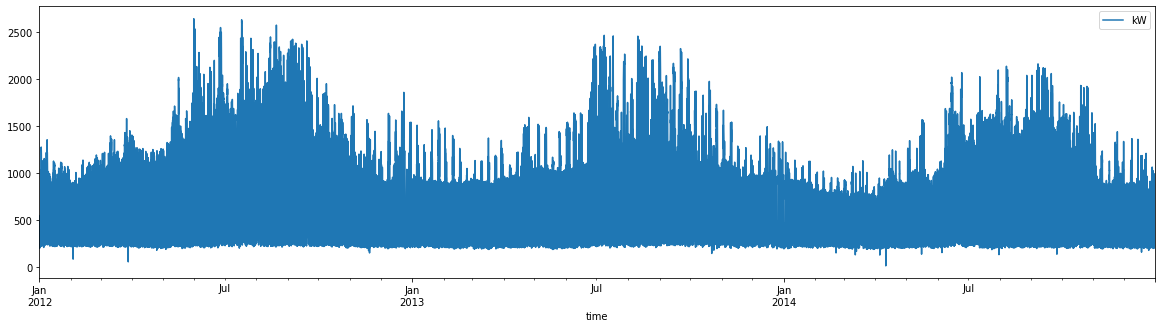
[7]:
# we'll apply a sqrt transformation and center before training, and inverse these for plotting/eval:
group_means = (df_elec
.assign(kW_sqrt = lambda df: np.sqrt(df['kW']))
.query("dataset=='train'")
.groupby('group')
['kW_sqrt'].mean()
.to_dict())
def add_transformed(df: pd.DataFrame) -> pd.DataFrame:
return df.assign(kW_sqrt_c = lambda df: np.sqrt(df['kW']) - df['group'].map(group_means))
def add_inv_transformed(df: pd.DataFrame) -> pd.DataFrame:
df = df.copy()
cols = [c for c in ['lower', 'upper', 'mean', 'actual'] if c in df.columns]
df[cols] += df['group'].map(group_means).to_numpy()[:, None]
df[cols] = df[cols].clip(lower=0) ** 2
if 'measure' in df.columns:
df['measure'] = df['measure'].str.replace('_sqrt_c', '')
return df
[8]:
df_elec = add_transformed(df_elec)
A Standard Forecasting Approach¶
First, let’s try a standard exponential-smoothing algorithm on one of the series.
[9]:
from torchcast.process import LocalTrend, Season
es = ExpSmoother(
measures=['kW_sqrt_c'],
processes=[
# seasonal processes:
Season(id='day_in_week', period=24 * 7, dt_unit='h', K=3, fixed=True),
Season(id='day_in_year', period=24 * 365.25, dt_unit='h', K=8, fixed=True),
Season(id='hour_in_day', period=24, dt_unit='h', K=8, fixed=True),
# long-running trend:
LocalTrend(id='trend'),
]
)
[10]:
ds_example_building = TimeSeriesDataset.from_dataframe(
df_elec.query("group == @example_group"),
group_colname='group',
time_colname='time',
dt_unit='h',
measure_colnames=['kW_sqrt_c'],
)
ds_example_train, _ = ds_example_building.train_val_split(dt=SPLIT_DT)
ds_example_train
[10]:
TimeSeriesDataset(sizes=[torch.Size([1, 12408, 1])], measures=(('kW_sqrt_c',),))
[11]:
es.fit(
ds_example_train.tensors[0],
start_offsets=ds_example_train.start_datetimes,
)
Initializing trend.position to -3.935213044314878e-08
[11]:
ExpSmoother(processes=[Season(id='day_in_week'), Season(id='day_in_year'), Season(id='hour_in_day'), LocalTrend(id='trend')], measures=['kW_sqrt_c'])
Visualizing the results is… not that illuminating:
[16]:
es_predictions = es(
ds_example_train.tensors[0],
start_offsets=ds_example_train.start_datetimes,
# note we *not* getting `num_timesteps` from `ds_example_train`, since we want to forecast outside the training time:
out_timesteps=ds_example_building.num_timesteps
)
es_predictions.plot(es_predictions.to_dataframe(ds_example_train), split_dt=SPLIT_DT)
/Users/jacobdink/miniconda3/envs/windcreek-labs/lib/python3.9/site-packages/plotnine/geoms/geom_path.py:100: PlotnineWarning: geom_path: Removed 13896 rows containing missing values.
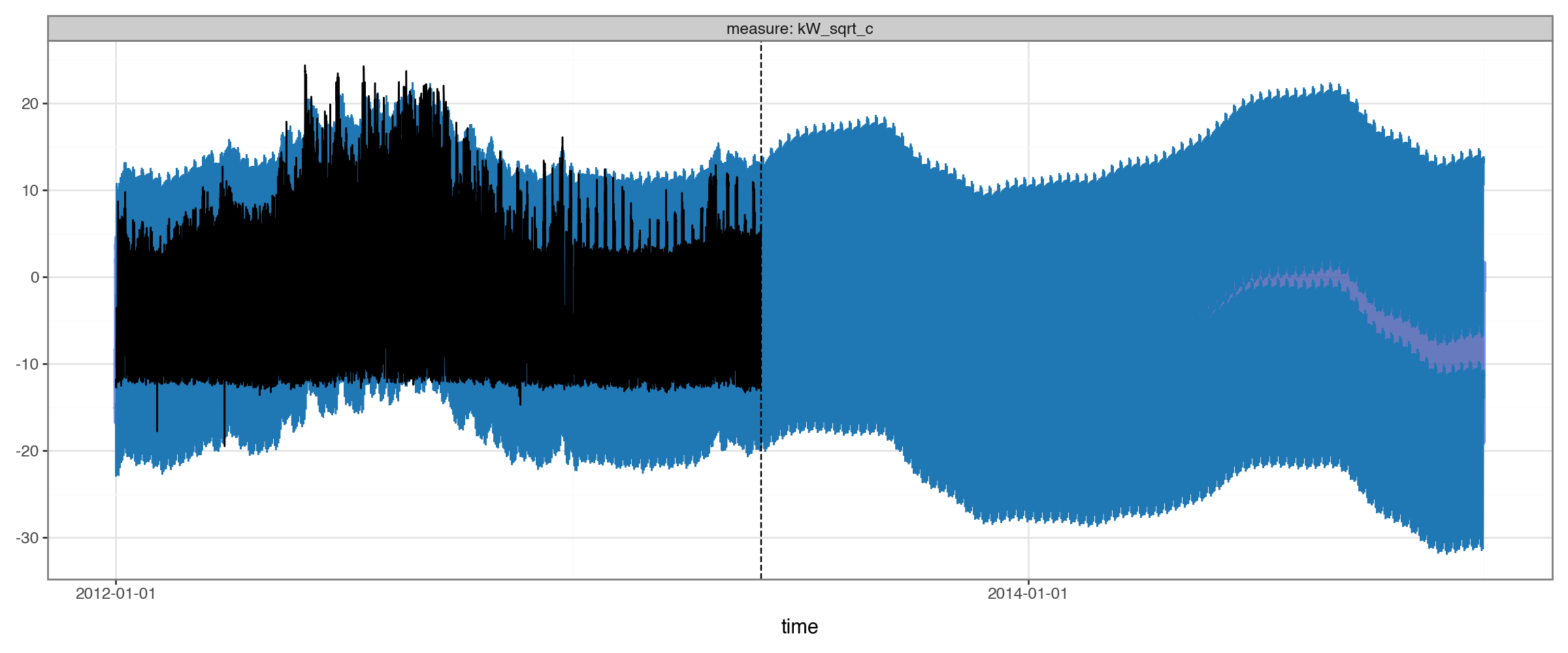
With hourly data, it’s just really hard to see the data when we are this zoomed out!
We can try zooming in:
[17]:
es_predictions.plot(
es_predictions
.to_dataframe(ds_example_building).query("time.between('2013-05-15', '2013-06-15')")
.pipe(add_inv_transformed),
split_dt=SPLIT_DT
)
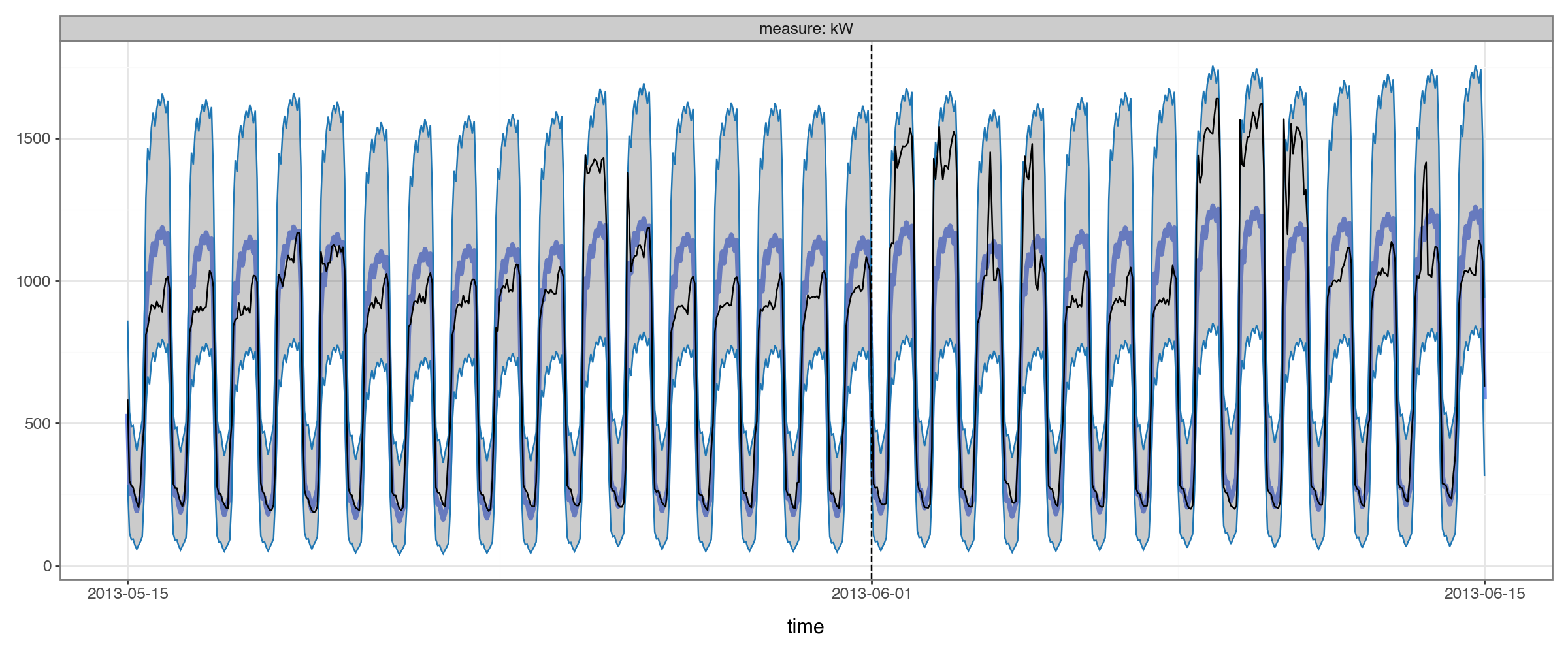
This is better for actually seeing the data, but ideally we’d still like to get a view of the long range.
Let’s instead try splitting it into weekdays vs. weekends and daytimes vs. nightimes:
[18]:
def plot_2x2(df: pd.DataFrame,
pred_colname: str = 'mean',
actual_colname: str = 'actual',
group_colname: str = 'group',
time_colname: str = 'time',
**kwargs):
"""
Plot predicted vs. actual for a single group, splitting into 2x2 facets of weekday/end * day/night.
"""
df_plot = df.assign(
time_of_day=None,
weekend=lambda df: np.where(df[time_colname].dt.weekday.isin([5, 6]), 'weekend', 'weekday'),
date=lambda df: df[time_colname].dt.normalize()
)
df_plot.loc[df_plot[time_colname].dt.hour.isin([14, 15, 16, 17, 18]), 'time_of_day'] = 'day'
df_plot.loc[df_plot[time_colname].dt.hour.isin([2, 3, 4, 5, 6]), 'time_of_day'] = 'night'
df_plot[time_colname] = df_plot.pop('date')
_agg = [pred_colname, actual_colname]
if 'upper' in df_plot.columns:
_agg.extend(['upper', 'lower'])
df_plot = df_plot.groupby([group_colname, time_colname, 'weekend', 'time_of_day'])[_agg].mean().reset_index()
df_plot['measure'] = df_plot['weekend'] + ' ' + df_plot['time_of_day']
df_plot['mean'] = df_plot.pop(pred_colname)
df_plot['actual'] = df_plot.pop(actual_colname)
if 'upper' not in df_plot.columns:
df_plot['lower'] = df_plot['upper'] = float('nan')
return Predictions.plot(df_plot, time_colname=time_colname, group_colname=group_colname, **kwargs) + facet_wrap('measure')
[19]:
plot_2x2(es_predictions
.to_dataframe(ds_example_building)
.pipe(add_inv_transformed)
,split_dt=SPLIT_DT)
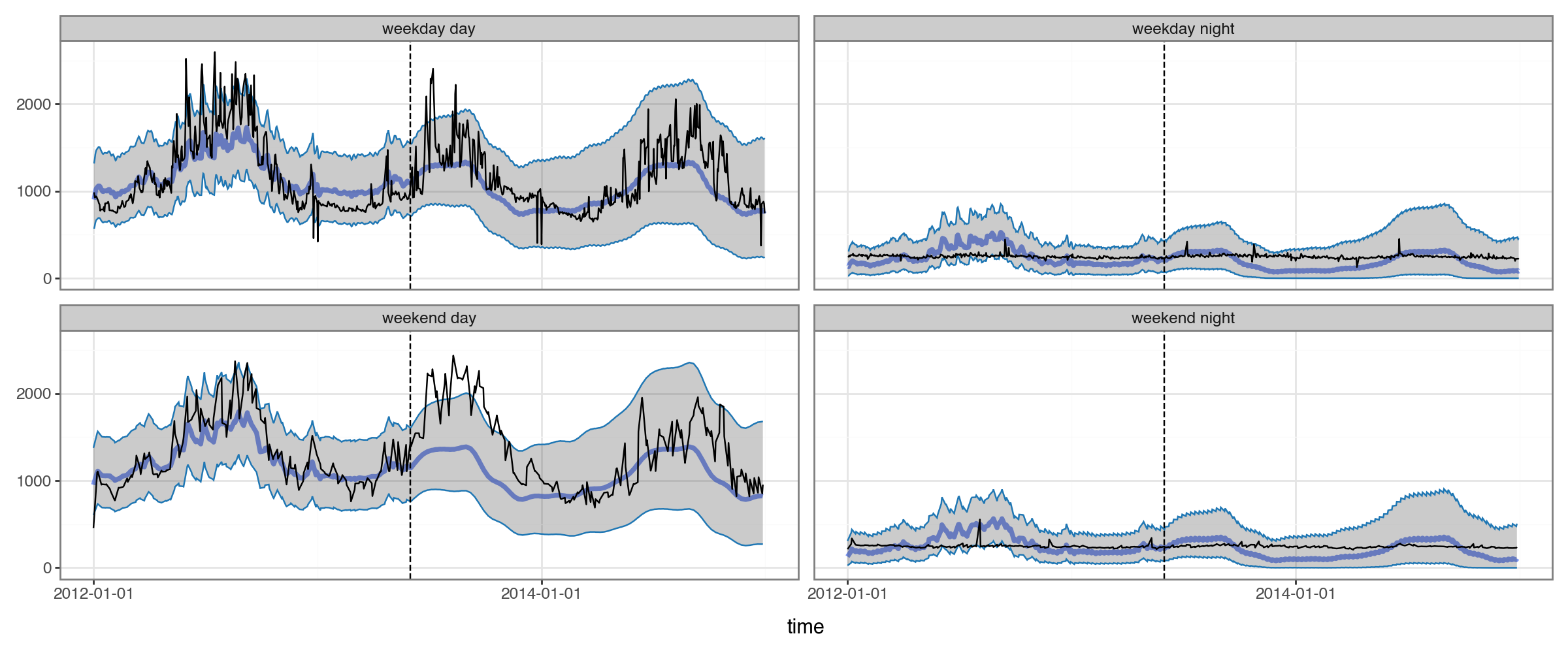
Viewing the forecasts in this way helps us see a serious issue: the annual seasonal pattern is very different for daytimes and nighttimes, but the model isn’t capturing that at all. (In fact, even the lower amplitude in annual seasonality for nighttime forecasts is just an artifact of our sqrt-transform, not a product of the model.)
The limitation is inherent to the model: it only allows for a single seasonal pattern, rather than a separate one for different times of the day and days of the week.
Incorporating a Neural Network¶
We saw our time-series model wasn’t allowing for interactions among the components of our time-series model. A natural solution to this is to incorporate a neural network – learning arbitrary/complex interactions is exactly what they are for.
Of course, this requires scaling up our dataset: we want to learn across multiple series, so that our network can build representations of patterns that are shared across multiple buildings.
Encoding Seasonlity as Fourier Terms¶
We’re going to need to encode the seasonal cycles in our data into features that a neural-network can use as inputs.
There are multiple ways we can do this. For example, one option would be to extract each component of our datetimes and one-hot encode it:
[20]:
(df_elec
.loc[df_elec['group']==example_group,['time']]
.assign(hod=lambda df: df['time'].dt.hour, dow=lambda df: df['time'].dt.dayofweek)
.pipe(pd.get_dummies, columns=['hod', 'dow'], dtype='float')
.head())
[20]:
| time | hod_0 | hod_1 | hod_2 | hod_3 | hod_4 | hod_5 | hod_6 | hod_7 | hod_8 | ... | hod_21 | hod_22 | hod_23 | dow_0 | dow_1 | dow_2 | dow_3 | dow_4 | dow_5 | dow_6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9232450 | 2012-01-01 00:00:00 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 9232451 | 2012-01-01 01:00:00 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 9232452 | 2012-01-01 02:00:00 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 9232453 | 2012-01-01 03:00:00 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 9232454 | 2012-01-01 04:00:00 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
5 rows × 32 columns
Instead, we’ll use a different approach based on fourier series. Basically, we encoded our times into sine/cosine waves. The number of waves is a hyper-parameter that can be tuned and helps us control how ‘wiggly’ we’ll allow the seasons to be. For more reading on using fourier series for modeling seasonality, see here and here.
For visualization (and shortly, modeling), we’ll use torchcast’s add_season_features function:
[21]:
from torchcast.utils import add_season_features
df_example = (df_elec[df_elec['group'] == example_group]
.reset_index(drop=True)
.pipe(add_season_features, K=8, period='yearly')
.pipe(add_season_features, K=3, period='weekly')
.pipe(add_season_features, K=8, period='daily'))
yearly_season_feats = df_example.columns[df_example.columns.str.startswith('yearly_')].tolist()
weekly_season_feats = df_example.columns[df_example.columns.str.startswith('weekly_')].tolist()
daily_season_feats = df_example.columns[df_example.columns.str.startswith('daily_')].tolist()
season_feats = yearly_season_feats + weekly_season_feats + daily_season_feats
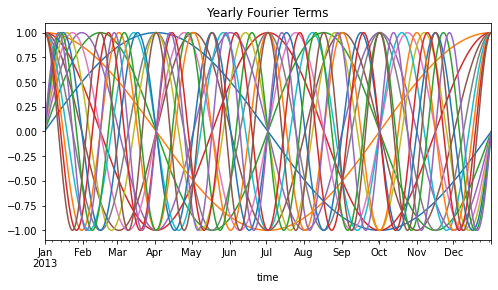
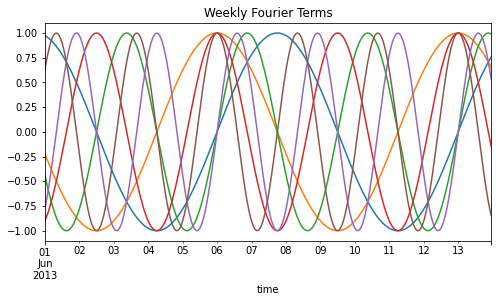
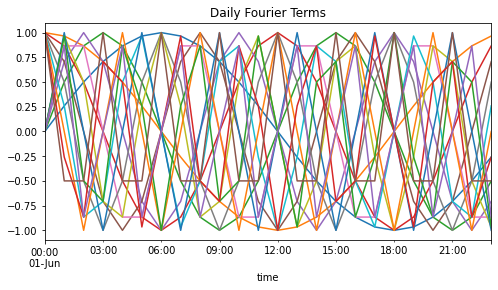
Let’s visualize these waves:
[22]:
(df_example[yearly_season_feats + ['time']]
.query("time.dt.year == 2013")
.plot(x='time', figsize=(8,4), legend=False, title='Yearly Fourier Terms'))
(df_example[weekly_season_feats + ['time']]
.query("(time.dt.year == 2013) & (time.dt.month == 6) & (time.dt.day < 14)")
.plot(x='time', figsize=(8,4), legend=False, title='Weekly Fourier Terms'))
(df_example[daily_season_feats + ['time']]
.query("(time.dt.year == 2013) & (time.dt.month == 6) & (time.dt.day == 1)")
.plot(x='time', figsize=(8,4), legend=False, title='Daily Fourier Terms'))
[22]:
<Axes: title={'center': 'Daily Fourier Terms'}, xlabel='time'>
Step 1: Pre-Training a Seasonal-Embeddings NN¶
For this task, we’ll switch from exponential smoothing (with ExpSmoother) to a full state-space model (with KalmanFilter). This is because only the latter can learn relationships specific to each time-series.
The LinearModel provides a catch-all for any way of passing arbitrary inputs to our model. For example, if we had weather data – temperature, humidity, wind-speed – we might add a process like:
LinearModel(id='weather', predictors=['temp','rhumidity','windspeed'])
And our time-series model would learn how each of these impacts our series(es).
Here we are using LinearModel a little differently: rather than it taking as input predictors, it will take as input the output of a neural-network, which itself will take predictors (the calendar-features we just defined).
What we’d like to do is train a neural network to embed the seasonality (as represented by our fourier terms) into a lower dimensional space, then we’ll pass that lower dimensional representation onto our KalmanFilter/LinearModel, which will learn how each time-series behaves in relation to that space. Basically, we are reducing the dozens of calendar-features (and their hundreds of interactions) into an efficient low-dimensional representation.
For this purpose, torchcast provides the SeasonalEmbeddingsTrainer class:
[23]:
from torchcast.utils.training import SeasonalEmbeddingsTrainer
SEASON_EMBED_NDIM = 20
season_embedder = torch.nn.Sequential(
torch.nn.LazyLinear(out_features=48),
torch.nn.Tanh(),
torch.nn.Linear(48, 48),
torch.nn.Tanh(),
torch.nn.Linear(48, SEASON_EMBED_NDIM)
)
season_trainer = SeasonalEmbeddingsTrainer(
module=season_embedder,
yearly=8,
weekly=3,
daily=8
)
Again, the number of embedding dimensions is a hyper-parameter, where we trade off computational efficiency for precision.
Since we’ll be training on the whole dataset instead of just one example building, we’ll switch from a TimeSeriesDataset to a TimeSeriesDataLoader, which lets us iterate over the whole dataset in a training loop:
[24]:
season_dl = TimeSeriesDataLoader.from_dataframe(
df_elec.query("dataset=='train'"),
group_colname='group',
time_colname='time',
dt_unit='h',
measure_colnames=['kW_sqrt_c'],
batch_size=45 # fairly even batch sizes
)
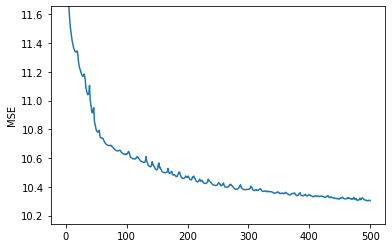
Let’s use our trainer to train season_embedder:
[25]:
try:
_path = os.path.join(BASE_DIR, f"season_trainer{SEASON_EMBED_NDIM}.pt")
with open(_path, 'rb') as f:
season_trainer = pickle.load(f).to(DEVICE)
season_embedder = season_trainer.module
plt.plot(season_trainer.loss_history)
plt.ylim(None, max(season_trainer.loss_history[5:]))
plt.ylabel('MSE')
plt.show()
except FileNotFoundError as e:
from IPython.display import clear_output
season_trainer.loss_history = []
for loss in season_trainer(season_dl):
season_trainer.loss_history.append(loss)
# plot:
if len(season_trainer.loss_history) > 5:
clear_output(wait=True)
plt.plot(season_trainer.loss_history)
plt.ylim(None, max(season_trainer.loss_history[5:]))
plt.ylabel('MSE')
plt.show()
if len(season_trainer.loss_history) > 500:
break
with open(_path, 'wb') as f:
pickle.dump(season_trainer, f)
season_trainer.to(torch.device('cpu'))
[25]:
<torchcast.utils.training.SeasonalEmbeddingsTrainer at 0x17e1dd8e0>
Let’s visualize the output of this neural network, with each color being a separate output:
[26]:
with torch.no_grad():
times = ds_example_building.times().squeeze()
pred = season_trainer.module(season_trainer.times_to_model_mat(times).to(torch.float))
_df_pred = pd.DataFrame(pred.numpy()).assign(time=times)
(_df_pred
.query("(time.dt.year == 2013) & (time.dt.month == 6) & (time.dt.day < 7)")
.plot(x='time', figsize=(10,5), legend=False, title=f'Season NN (dim={SEASON_EMBED_NDIM}) Output', alpha=0.5))
(_df_pred
.query("(time.dt.year == 2013) & (time.dt.month < 6)")
.plot(x='time', figsize=(10,5), legend=False, title=f'Season NN (dim={SEASON_EMBED_NDIM}) Output', alpha=0.25))
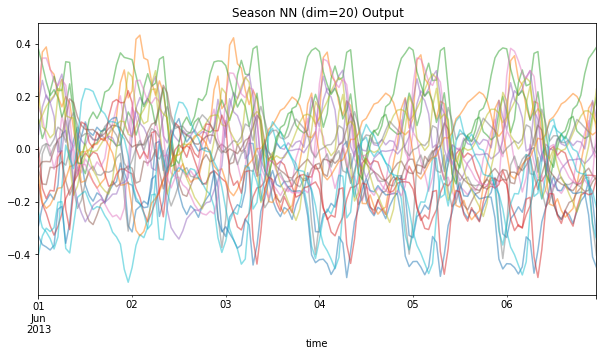
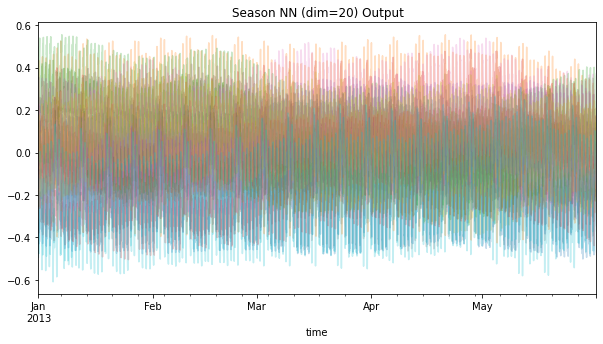
You can think of each colored line as equivalent to the sin/cos waves above; but now, instead of dozens of these, we have far fewer, that should hopefully be able to capture interacting seasonal effects.
Let’s verify this. The season-trainer has a predict method that lets us visualize how these embeddings can be used to predict the actual series values:
[27]:
with torch.no_grad():
display(ds_example_building
.to_dataframe()
.assign(pred=season_trainer.predict(ds_example_building).squeeze())
.pipe(plot_2x2, actual_colname='kW_sqrt_c', pred_colname='pred', split_dt=SPLIT_DT))
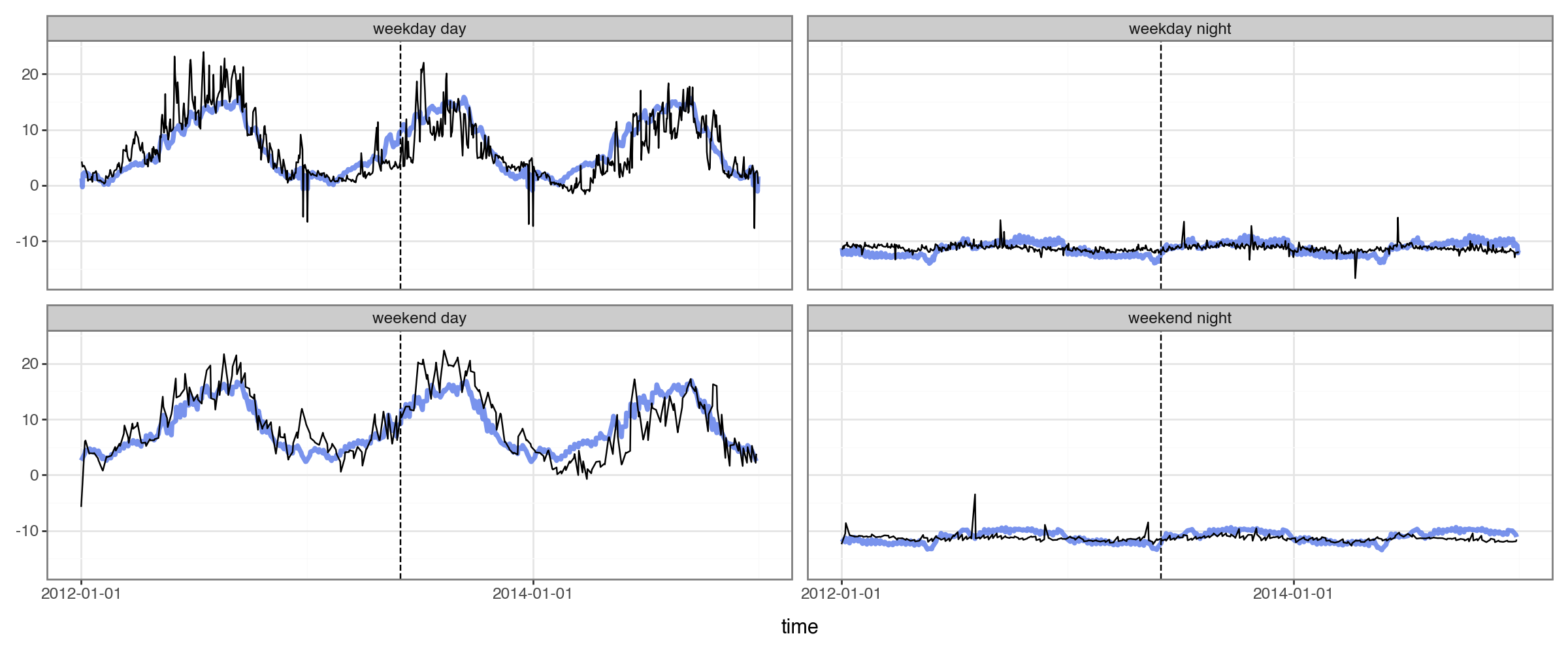
Success! We now have different seasonal patterns depending on the time of the day.
Step 2: Incorporate our Seasonal-Embeddings into our Time-Series Model¶
How should we incorporate our season_embedder neural-network into a state-space model? First, we create our time-series model:
[28]:
from torchcast.kalman_filter import KalmanFilter
from torchcast.process import LinearModel, LocalLevel
kf_nn = KalmanFilter(
measures=['kW_sqrt_c'],
processes=[
LinearModel(id='nn_output', predictors=[f'nn{i}' for i in range(SEASON_EMBED_NDIM)]),
LocalLevel(id='level'),
],
).to(DEVICE)
Then, we have two options:
The first option is to create our fourier-features on the dataframe, and pass these as features into a dataloader.
[31]:
dataloader_kf_nn = TimeSeriesDataLoader.from_dataframe(
df_elec
.query("dataset=='train'")
.pipe(add_season_features, K=8, period='yearly')
.pipe(add_season_features, K=3, period='weekly')
.pipe(add_season_features, K=8, period='daily')
,
group_colname='group',
time_colname='time',
dt_unit='h',
y_colnames=['kW_sqrt_c'],
X_colnames=season_feats,
batch_size=50
)
…then we’d train our model with a tool like Pytorch Lightning. Torchcast also includes a simple tool for this, the StateSpaceTrainer:
[32]:
from torchcast.utils.training import StateSpaceTrainer
ss_trainer = StateSpaceTrainer(
module=kf_nn,
dataset_to_kwargs=lambda batch: {'X' : season_trainer.module(batch.tensors[1])},
)
## commented out since we're going with option 2 below
# for loss in ss_trainer(dataloader_kf_nn):
# print(loss)
# # etc...
An even simpler (though less general) option is just to leverage the util methods in the
SeasonalEmbeddingsTrainer, which handles converting aTimeSeriesDatasetinto a tensor of fourier terms:
[33]:
def dataset_to_kwargs(batch: TimeSeriesDataset) -> dict:
seasonX = season_trainer.times_to_model_mat(batch.times()).to(dtype=torch.float, device=DEVICE)
return {'X' : season_trainer.module(seasonX)}
ss_trainer = StateSpaceTrainer(
module=kf_nn,
dataset_to_kwargs=dataset_to_kwargs,
optimizer=torch.optim.Adam(kf_nn.parameters(), lr=.05)
)
Then we don’t need to use add_season_features when creating our data-loader, since season_trainer.times_to_model_mat will create them per-batch as needed (which will be much easier on our GPU’s memory):
[34]:
dataloader_kf_nn = TimeSeriesDataLoader.from_dataframe(
df_elec.query("dataset=='train'"),
group_colname='group',
time_colname='time',
dt_unit='h',
measure_colnames=['kW_sqrt_c'],
batch_size=40
)
Training End-to-End
Above, we never actually registered season_trainer.module as an attribute of our KalmanFilter (i.e. we didn’t do kf_nn.season_nn = season_trainer.module). This means that we won’t continue training the embeddings as we train our KalmanFilter. Why not? For that matter, why did we pre-train in the first place? Couldn’t we have just registered an untrained embeddings network and trained the whole thing end to end?
In practice, neural-networks have many more parameters and take many more epochs than our state-space models (and conversely, our state-space models are much slower to train per epoch). So it’s much more efficient to pre-train the network first. Then it’s up to us whether we want to continue training the network, or just freeze its weights (i.e. exclude it from the optimizer) and just train the state-space models’ parameters. Here we’re freezing them by not assigning the network as an
attribute (so that the parameters don’t get passed to when we run torch.optim.Adam(kf_nn.parameters(), lr=.05)).
[35]:
try:
_path = os.path.join(BASE_DIR, f"ss_trainer{SEASON_EMBED_NDIM}.pt")
with open(_path, 'rb') as f:
ss_trainer = pickle.load(f).to(DEVICE)
kf_nn = ss_trainer.module
plt.plot(ss_trainer.loss_history)
plt.show()
except FileNotFoundError as e:
torch.cuda.empty_cache()
ss_trainer.loss_history = []
for loss in ss_trainer(dataloader_kf_nn, forward_kwargs={'n_step' : 14*7*24, 'every_step' : False}):
ss_trainer.loss_history.append(loss)
print(loss)
with open(_path, 'wb') as f:
pickle.dump(ss_trainer, f)
if len(ss_trainer.loss_history) > 30:
break
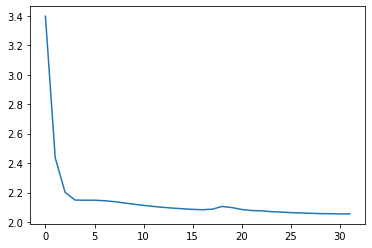
Now we’ll create forecasts for all the groups, and back-transform them, for plotting and evaluation.
[36]:
with torch.inference_mode():
dataloader_all = TimeSeriesDataLoader.from_dataframe(
# importantly, we'll set to `nan` our target when it's outside the training dates
# this allows us to use `season_feats` in the forecast period, while not having data-leakage
df_elec.assign(kW_sqrt_c=lambda df: df['kW_sqrt_c'].where(df['dataset']=='train')),
group_colname='group',
time_colname='time',
dt_unit='h',
measure_colnames=['kW_sqrt_c'],
batch_size=50
)
df_all_preds = []
for batch in tqdm(dataloader_all):
batch = batch.to(DEVICE)
seasonX = season_trainer.times_to_model_mat(batch.times()).to(dtype=torch.float, device=DEVICE)
pred = kf_nn(batch.tensors[0], X=season_trainer.module(seasonX), start_offsets=batch.start_offsets)
df_all_preds.append(pred.to_dataframe(batch).drop(columns=['actual']))
df_all_preds = pd.concat(df_all_preds).reset_index(drop=True)
# back-transform:
df_all_preds = (df_all_preds
.merge(df_elec[['group','time','kW','dataset']])
.pipe(add_inv_transformed))
df_all_preds
[36]:
| group | time | measure | mean | lower | upper | kW | dataset | |
|---|---|---|---|---|---|---|---|---|
| 0 | MT_001 | 2012-01-01 00:00:00 | kW | 1.082254 | 0.000000 | 133.029539 | 3.172589 | train |
| 1 | MT_001 | 2012-01-01 01:00:00 | kW | 0.310771 | 0.000000 | 36.109307 | 4.124365 | train |
| 2 | MT_001 | 2012-01-01 02:00:00 | kW | 1.107223 | 0.000000 | 33.909440 | 4.758883 | train |
| 3 | MT_001 | 2012-01-01 03:00:00 | kW | 2.929986 | 0.000000 | 38.848475 | 4.441624 | train |
| 4 | MT_001 | 2012-01-01 04:00:00 | kW | 3.193181 | 0.000000 | 37.979428 | 4.758883 | train |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 9548093 | MT_369 | 2014-12-31 19:00:00 | kW | 837.039001 | 476.854617 | 1297.890767 | 692.631965 | val |
| 9548094 | MT_369 | 2014-12-31 20:00:00 | kW | 827.793849 | 469.884445 | 1286.369644 | 688.416422 | val |
| 9548095 | MT_369 | 2014-12-31 21:00:00 | kW | 825.011579 | 467.799304 | 1282.883324 | 662.023460 | val |
| 9548096 | MT_369 | 2014-12-31 22:00:00 | kW | 836.415516 | 476.405873 | 1297.078379 | 679.252199 | val |
| 9548097 | MT_369 | 2014-12-31 23:00:00 | kW | 834.971269 | 475.314866 | 1295.281680 | 659.274194 | val |
9548098 rows × 8 columns
[37]:
plot_2x2(df_all_preds.query("group==@example_group"), actual_colname='kW', split_dt=SPLIT_DT)
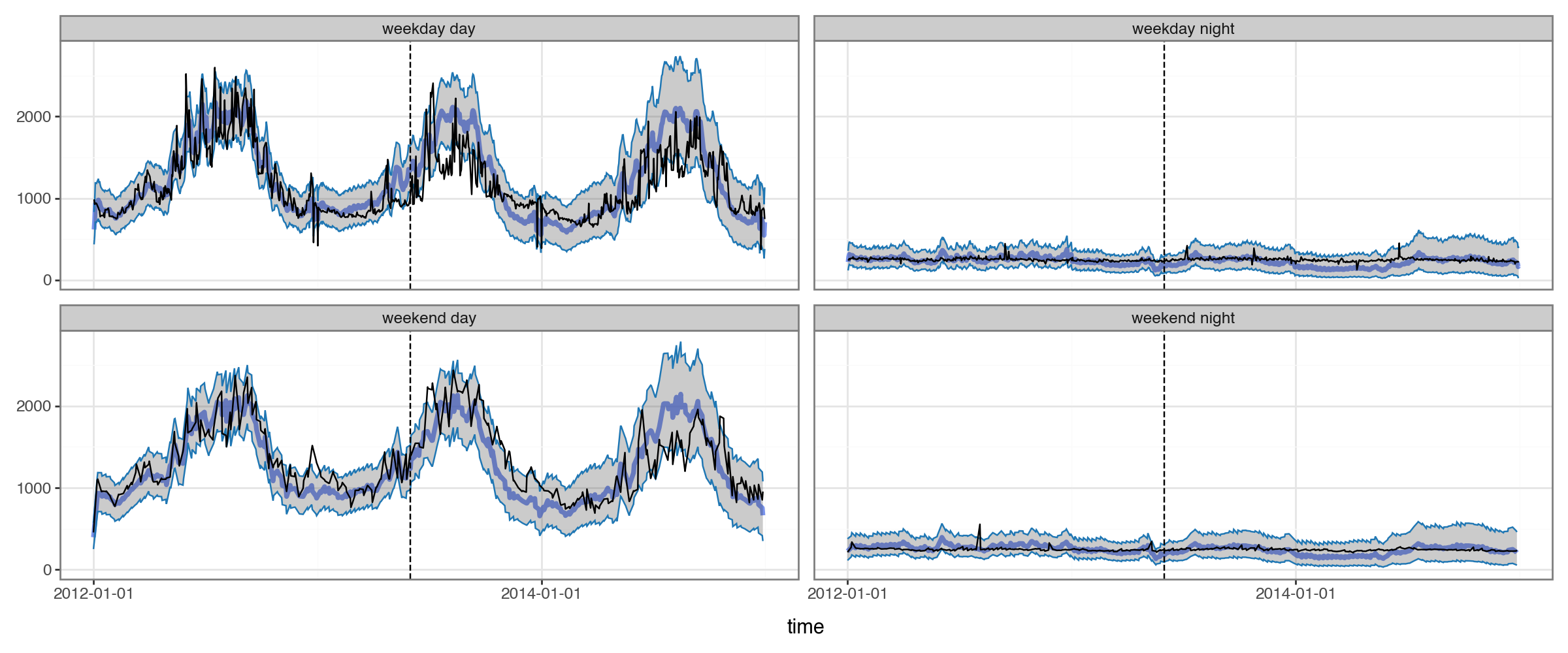
Success! If our example group is representative, our forecasting model was able to use the embeddings to capture complex seasonal structure.
Evaluation¶
A Simple Baseline¶
We’ve see that, for this dataset, generating forecasts that are sane is already an achievement.
But of course, ideally we’d actually have some kind of a quantitative measure of how good our forecasts are.
For this, it’s helpful to compare to a baseline. torchcast provides a simple baseline which just forecasts based on N-timesteps ago, with options for first smoothing the historical data. In this case, we forecast based on the same timepoint 365 days ago, after first applying a rolling-average with a 4-hour window.
[38]:
from torchcast.utils import make_baseline
df_baseline365 = make_baseline(df_elec,
group_colnames=['group'],
time_colname='time',
value_colname='kW',
is_train=lambda df: df['dataset']=='train',
lag=int(365*24),
smooth=4)
plot_2x2(
df_baseline365.query("group==@example_group").merge(df_elec),
pred_colname='baseline',
actual_colname='kW',
split_dt=SPLIT_DT
)
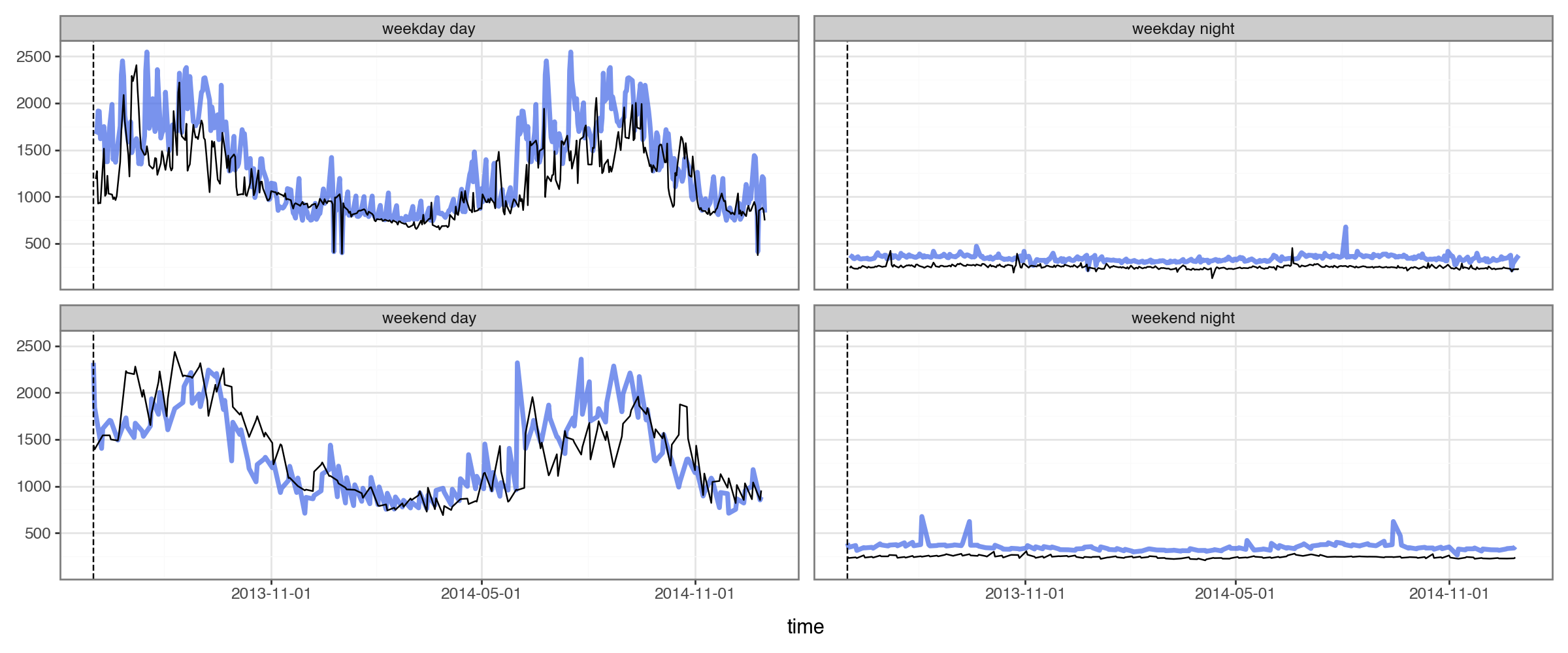
We can see this baseline provides sensible enough forecasts on our example building.
Comparison of Performance¶
Now that we have something to compare our torchcast model to, we can evaluate its performance.
[39]:
df_compare = (df_all_preds[['group', 'mean', 'time', 'kW', 'dataset']]
.rename(columns={'mean' : 'torchcast'})
.merge(df_baseline365, how='left'))
df_compare_long = df_compare.melt(
id_vars=['group', 'time', 'kW', 'dataset'],
value_vars=['torchcast', 'baseline'],
var_name='model',
value_name='forecast'
)
df_compare_long['error'] = np.abs(df_compare_long['forecast'] - df_compare_long['kW'])
df_compare_long
[39]:
| group | time | kW | dataset | model | forecast | error | |
|---|---|---|---|---|---|---|---|
| 0 | MT_001 | 2012-01-01 00:00:00 | 3.172589 | train | torchcast | 1.082254 | 2.090335 |
| 1 | MT_001 | 2012-01-01 01:00:00 | 4.124365 | train | torchcast | 0.310771 | 3.813595 |
| 2 | MT_001 | 2012-01-01 02:00:00 | 4.758883 | train | torchcast | 1.107223 | 3.651660 |
| 3 | MT_001 | 2012-01-01 03:00:00 | 4.441624 | train | torchcast | 2.929986 | 1.511639 |
| 4 | MT_001 | 2012-01-01 04:00:00 | 4.758883 | train | torchcast | 3.193181 | 1.565702 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 19096191 | MT_369 | 2014-12-31 19:00:00 | 692.631965 | val | baseline | 712.793255 | 20.161290 |
| 19096192 | MT_369 | 2014-12-31 20:00:00 | 688.416422 | val | baseline | 702.025293 | 13.608871 |
| 19096193 | MT_369 | 2014-12-31 21:00:00 | 662.023460 | val | baseline | 708.486070 | 46.462610 |
| 19096194 | MT_369 | 2014-12-31 22:00:00 | 679.252199 | val | baseline | 728.464076 | 49.211877 |
| 19096195 | MT_369 | 2014-12-31 23:00:00 | 659.274194 | val | baseline | 751.282991 | 92.008798 |
19096196 rows × 7 columns
Over Time
First let’s compare abs(error) over time, across all groups:
[40]:
df_compare_per_date = (df_compare_long
.query("dataset!='train'")
.assign(date=lambda df: df['time'].dt.normalize())
.groupby(['date', 'model'])
['error'].mean()
.reset_index())
(df_compare_per_date
.pivot(index='date', columns='model', values='error')
.plot(ylim=(0, 300), ylabel="Abs(Error)", title="Torchcast vs. Baseline: Error over Time"))
[40]:
<Axes: title={'center': 'Torchcast vs. Baseline: Error over Time'}, xlabel='date', ylabel='Abs(Error)'>
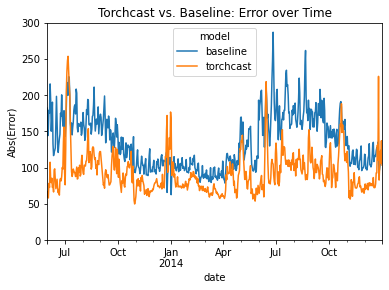
We can see that the torchcast model beats the baseline almost ever day. The clear exception is holidays (e.g. Thanksgiving and Christmas), which makes sense: we didn’t add any features for these to our torchcast model, while the baseline model essentially gets these for free. Future attempts could resolve this straightforwardly by adding dummy-features to our LinearModel, or by increasing the K (aka “wiggliness”) parameter (see “Encoding Seasonlity as Fourier Terms” above).
By Group
Now let’s compare over the whole test period, focusing on percent error (relative to that group’s average) so that we can weight small and large groups equally.
[41]:
from matplotlib.ticker import PercentFormatter
df_compare_per_group = (df_compare_long
.groupby(['group', 'dataset', 'model'])
[['error', 'kW']].mean()
.reset_index()
.assign(prop_error=lambda df: df['error'] / df['kW']))
compare_per_group_agg = (df_compare_per_group
.groupby(['dataset', 'model'])
.agg(prop_error=('prop_error', 'mean'), sem=('prop_error', 'sem')))
(compare_per_group_agg.loc['test']['prop_error']
.plot(kind='bar',
yerr=compare_per_group_agg.loc['test']['sem'],
ylabel='Percent Error',
title="Torchcast vs. Baseline: % Error in Test Set")
.yaxis.set_major_formatter(PercentFormatter(xmax=1)))
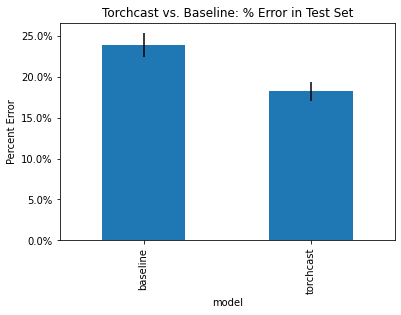
We see that the torchcast forecasts have significantly lower % error on average.