Multivariate Forecasts: Beijing Multi-Site Air-Quality Data¶

We’ll demonstrate several features of torchcast using a dataset from the UCI Machine Learning Data Repository. It includes data on air pollutants and weather from 12 sites.

[3]:

df_aq = load_air_quality_data('daily')

SPLIT_DT = np.datetime64('2016-02-22')
df_aq['dataset'] = np.where(df_aq['date'] > SPLIT_DT, 'val', 'train')
df_aq

[3]:

	date	station	PM2p5	PM10	SO2	NO2	CO	O3	TEMP	PRES	DEWP	RAIN	WSPM	dataset
0	2013-03-01	Aotizhongxin	7.125000	10.750000	11.708333	22.583333	429.166667	63.875000	1.391667	1026.875000	-18.745833	0.0	3.254167	train
1	2013-03-01	Changping	5.083333	18.958333	16.041667	15.333333	387.500000	77.791667	0.812500	1023.858333	-19.583333	0.0	2.133333	train
2	2013-03-01	Dingling	6.375000	6.409091	3.000000	2.625000	204.166667	81.958333	0.812500	1023.858333	-19.583333	0.0	2.133333	train
3	2013-03-01	Dongsi	6.416667	9.875000	8.478261	28.521739	395.652174	72.782609	1.325000	1028.783333	-21.466667	0.0	3.308333	train
4	2013-03-01	Guanyuan	7.541667	11.666667	8.500000	28.500000	400.000000	63.166667	1.391667	1026.875000	-18.745833	0.0	3.254167	train
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
17527	2017-02-28	Nongzhanguan	17.523810	24.739130	7.347826	35.652174	526.086957	56.086957	10.958333	1014.887500	-12.783333	0.0	2.058333	val
17528	2017-02-28	Shunyi	20.708333	28.500000	7.125000	39.666667	579.166667	57.291667	9.250000	1015.550000	-10.429167	0.0	2.025000	val
17529	2017-02-28	Tiantan	14.875000	32.708333	6.454545	42.904762	540.909091	57.600000	10.958333	1014.887500	-12.783333	0.0	2.058333	val
17530	2017-02-28	Wanliu	9.958333	25.583333	7.458333	40.916667	479.166667	54.791667	10.516667	1013.345833	-12.266667	0.0	1.800000	val
17531	2017-02-28	Wanshouxigong	10.958333	21.541667	4.956522	31.391304	530.434783	54.913043	10.958333	1014.887500	-12.783333	0.0	2.058333	val

17532 rows × 14 columns

Univariate Forecasts¶

Let’s build a model to predict total particulate-matter (PM2.5 and PM10).

First, we’ll make our target the sum of these two types. We’ll log-transform since this is strictly positive.

[4]:

df_aq['PM'] = df_aq['PM10'] + df_aq['PM2p5']
df_aq['PM_log10'] = np.log10(df_aq['PM'])

[5]:

# create our dataset:
dataset_pm = TimeSeriesDataset.from_dataframe(
    dataframe=df_aq,
    dt_unit='D',
    measure_colnames=['PM_log10'],
    group_colname='station',
    time_colname='date'
)
dataset_pm_train, _ = dataset_pm.train_val_split(dt=SPLIT_DT)

[6]:

# specify our model:
from torchcast.process import LocalTrend, Season

kf_pm = KalmanFilter(
    measures=['PM_log10'],
    processes=[
        LocalTrend(id='trend'),
        Season(
            id='day_in_year',
            period=365.25,
            dt_unit='D',
            K=4,
            fixed=True
        ),
        Season(
            id='day_in_week',
            period=7,
            dt_unit='D',
            K=2,
            fixed=True
        )
    ]
)

[7]:

# fit it:
kf_pm.fit(
    dataset_pm_train.tensors[0],
    start_offsets=dataset_pm_train.start_datetimes,
    n_step=5, every_step=False
)

Initializing trend.position to 2.152986526489258

[7]:

KalmanFilter(processes=[LocalTrend(id='trend'), Season(id='day_in_year'), Season(id='day_in_week')], measures=['PM_log10'])

The n_step argument

When fitting our model, we use the n_step argument to improve longer-range forecasts. We know we will be using our model to forecast weeks/months into the future, so we ‘encourage’ the model to get good at this task by optimizing for 5-step-ahead forecasts (rather than the traditional 1-step-ahead forecasts) in training.

This simple strategy can often dramatically improve the quality of long-range forecasts; and paired with the every_step=False setting, does not cause an increase in training-time.

Let’s see how our forecasts look:

[8]:

# helper for transforming log back to original:
def inverse_transform(df: pd.DataFrame) -> pd.DataFrame:
    df = df.copy()
    # bias-correction for log-transform (see https://otexts.com/fpp2/transformations.html#bias-adjustments)
    df['mean'] = df['mean'] + .5 * df['std'] ** 2
    df['lower'] = df['mean'] - 1.96 * df['std']
    df['upper'] = df['mean'] + 1.96 * df['std']
    # inverse the log10:
    df[['actual', 'mean', 'upper', 'lower']] = 10 ** df[['actual', 'mean', 'upper', 'lower']]
    df['measure'] = df['measure'].str.replace('_log10', '')
    return df

[9]:

# generate forecasts:
forecast = kf_pm(
        dataset_pm_train.tensors[0],
        start_offsets=dataset_pm_train.start_datetimes,
        out_timesteps=dataset_pm.tensors[0].shape[1]
)

# convert to dataframe, back-transform:
df_uv_pred = (forecast
             .set_metadata(group_colname='station', time_colname='date')
             .to_dataframe(dataset_pm, conf=None)
             .pipe(inverse_transform))

# plot:
forecast.plot(
    df_uv_pred.query("date>'2014-01-01'"),
    max_num_groups=2,
    split_dt=SPLIT_DT,
    figure_size=(6,5)
)

Subsetting to groups: ['Aotizhongxin', 'Dingling']

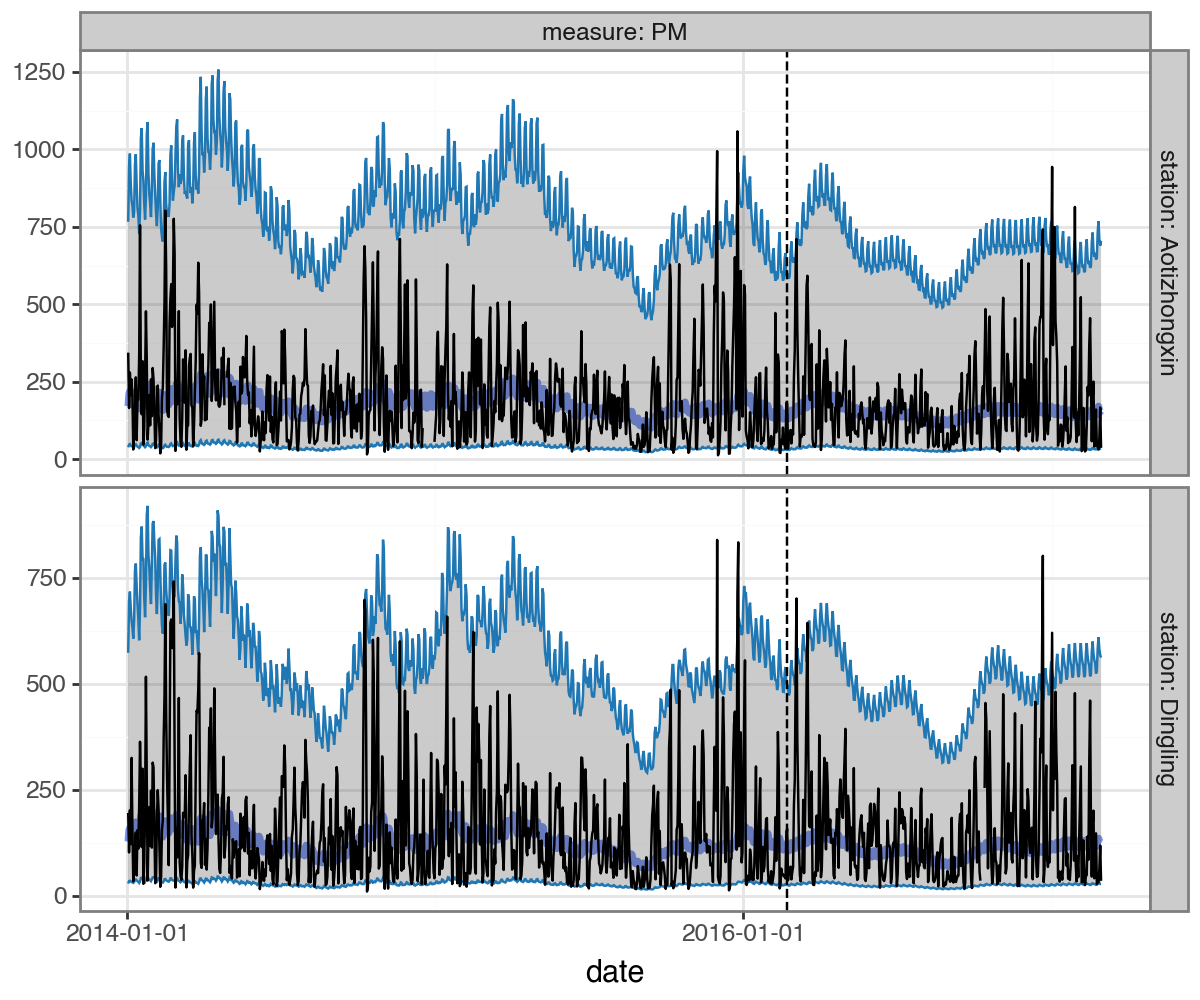
../_images/examples_air_quality_12_1.png

Multivariate Forecasts¶

Can we improve our model by splitting the pollutant we are forecasting into its two types (2.5 and 10), and modeling them in a multivariate manner?

[10]:

# create a dataset:
df_aq['PM10_log10'] = np.log10(df_aq['PM10'])
df_aq['PM2p5_log10'] = np.log10(df_aq['PM2p5'])
dataset_pm_mv = TimeSeriesDataset.from_dataframe(
    dataframe=df_aq,
    dt_unit='D',
    measure_colnames=['PM10_log10','PM2p5_log10'],
    group_colname='station',
    time_colname='date'
)
dataset_pm_mv_train, _ = dataset_pm_mv.train_val_split(dt=SPLIT_DT)

# create a model:
_processes = []
for m in dataset_pm_mv.measures[0]:
    _processes.extend([
        LocalTrend(id=f'{m}_trend', measure=m),
        Season(
            id=f'{m}_day_in_year',
            period=365.25,
            dt_unit='D',
            K=4,
            measure=m,
            fixed=True
        ),

        Season(
            id=f'{m}_day_in_week',
            period=7,
            dt_unit='D',
            K=2,
            measure=m,
            fixed=True
        )
    ])
kf_pm_mv = KalmanFilter(
    measures=dataset_pm_mv.measures[0],
    processes=_processes
)

# fit:
kf_pm_mv.fit(
    dataset_pm_mv_train.tensors[0],
    start_offsets=dataset_pm_mv_train.start_datetimes,
    n_step=5, every_step=False,
)

Initializing PM10_log10_trend.position to 1.9197293519973755
Initializing PM2p5_log10_trend.position to 1.7517921924591064

[10]:

KalmanFilter(processes=[LocalTrend(id='PM10_log10_trend'), Season(id='PM10_log10_day_in_year'), Season(id='PM10_log10_day_in_week'), LocalTrend(id='PM2p5_log10_trend'), Season(id='PM2p5_log10_day_in_year'), Season(id='PM2p5_log10_day_in_week')], measures=['PM10_log10', 'PM2p5_log10'])

Generate our forecasts as before:

[11]:

with torch.no_grad():
    forecast_mv = kf_pm_mv(
        dataset_pm_mv_train.tensors[0],
        start_offsets=dataset_pm_mv_train.start_datetimes,
        out_timesteps=dataset_pm_mv.num_timesteps # <--- how we ask it to forecast past original times
    )
forecast_mv.means.shape

[11]:

torch.Size([12, 1461, 2])

[12]:

forecast_mv.plot(
    forecast_mv
    .set_metadata(group_colname='station', time_colname='date')
    .to_dataframe(dataset_pm_mv, conf=None)
    .pipe(inverse_transform)
    .query("date>'2014-01-01'"),
    max_num_groups=2,
    split_dt=SPLIT_DT,
)

Subsetting to groups: ['Wanliu', 'Tiantan']

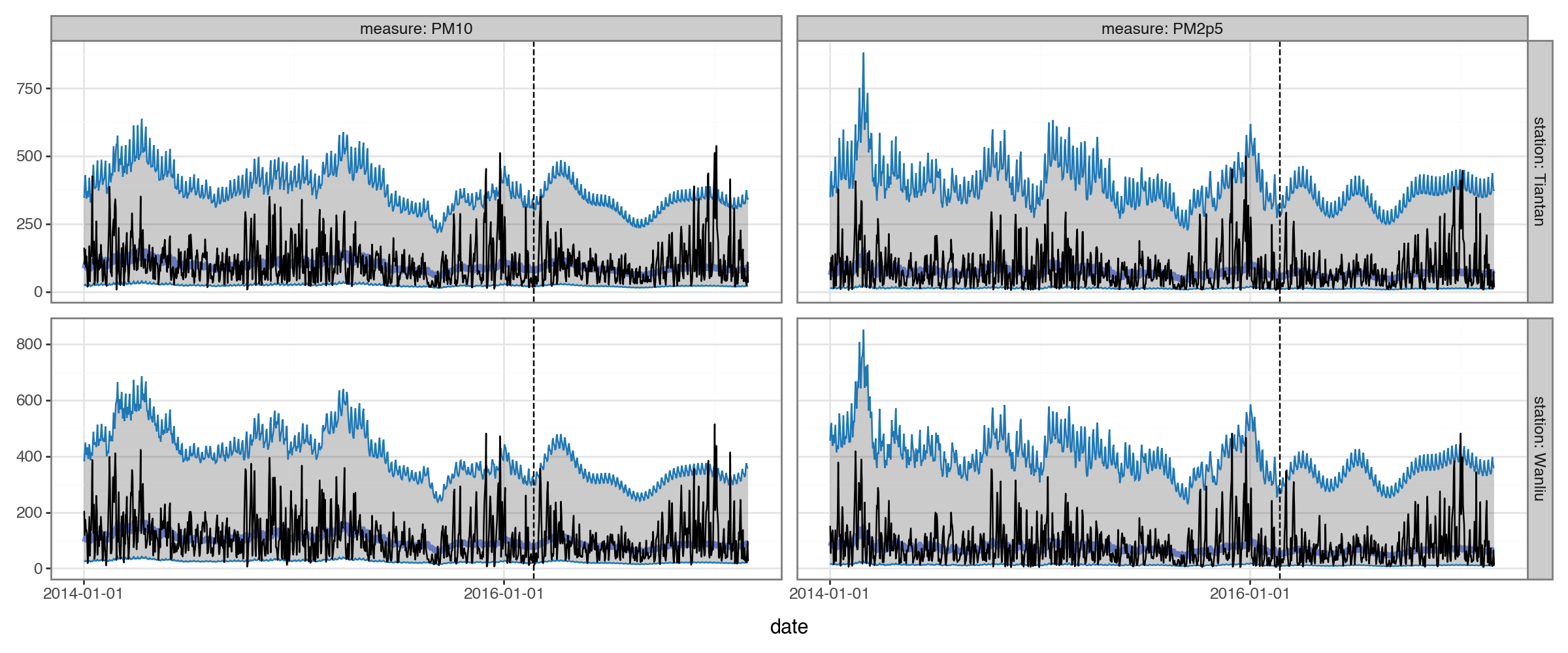
../_images/examples_air_quality_17_1.png

At this point, though, we run into a problem: we we have forecasts for both PM2.5 and PM10, but we ultimately want a forecast for their sum. With untransformed data, we could take advantage of the fact that sum of correlated normals is still normal; but we have log-transformed our measures. This seems like it was the right choice (i.e. our residuals look reasonably normal and i.i.d):

[13]:

forecast_mv.plot(
    forecast_mv
    .to_dataframe(dataset_pm_mv, type='components')
    .query("process=='residuals'")
    .query("date>'2014-01-01'"),
    figure_size=(6,5)
) + facet_wrap('measure', ncol=1)

Subsetting to groups: ['Wanshouxigong']

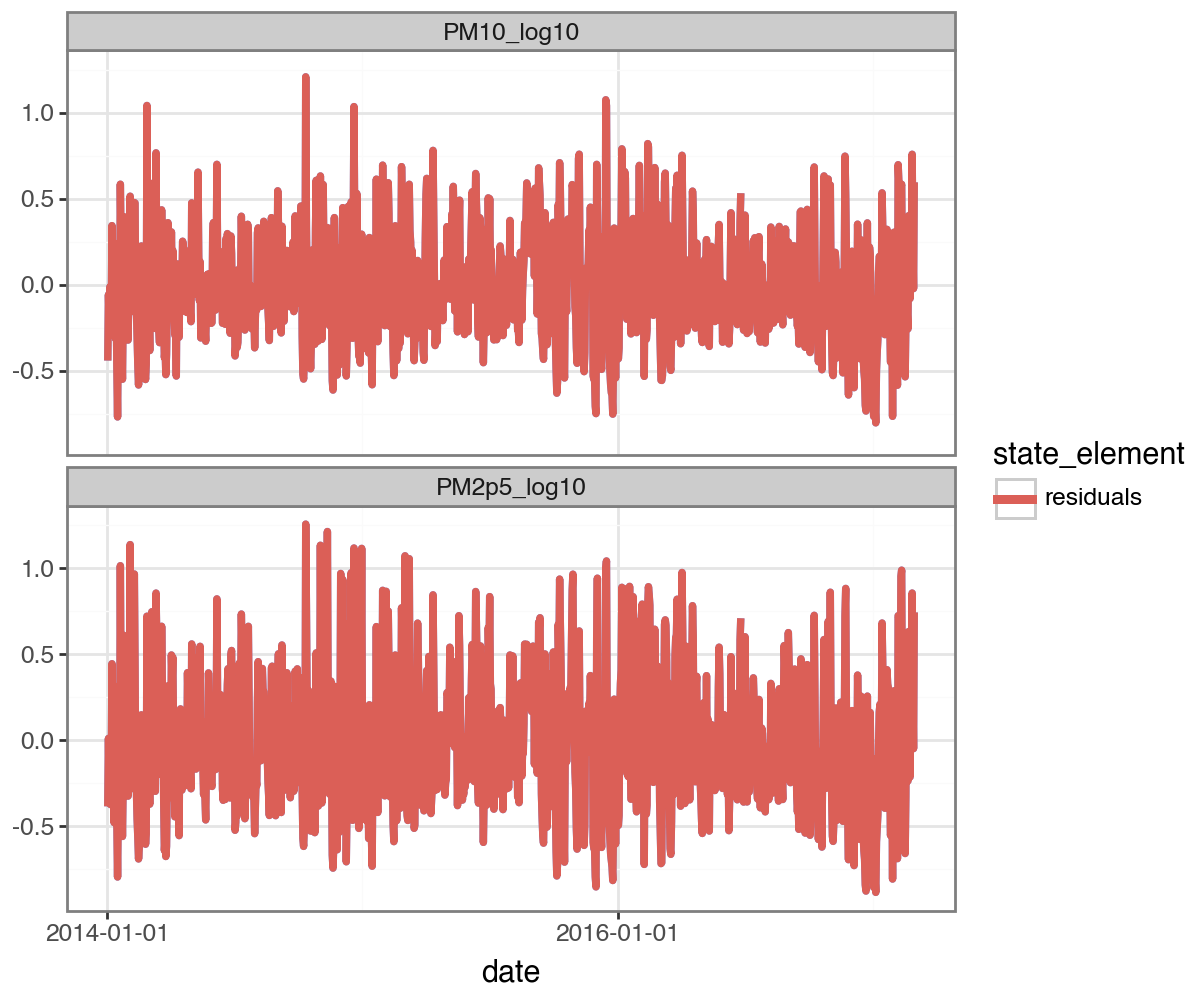
../_images/examples_air_quality_19_1.png

In this case, we can’t take the sum of our forecasts to get the forecast of the sum, and there’s no simple closed-form expression for the sum of lognormals.

One option that is fairly easy in torchcast is to use a Monte-Carlo approach: we’ll just generate random-samples based on the means and covariances underlying our forecast. In that case, the sum of the PM2.5 + PM10 forecasted-samples is the forecasted PM sum we are looking for:

[14]:

@torch.no_grad()
def sum_mc_preds_as_df(preds: Predictions,
                          dataset: TimeSeriesDataset,
                          inverse_transform_fun: callable,
                          num_draws: int = 1000,
                          **kwargs) -> pd.DataFrame:
    """
    Our predictions are on the transformed scale, and we'd like to sum across measures on the original scale;
    this function uses a monte-carlo approach to do this.
    """
    # generate draws from the forecast distribution, apply inverse-transform:
    mean, cov = preds
    eps = 1e-6 * torch.eye(cov.shape[-1]).unsqueeze(0).unsqueeze(0) # handle numerical instability
    mc_draws = torch.distributions.MultivariateNormal(mean, cov + eps, validate_args=False).rsample((num_draws,))
    # sum across measures (e.g. 2.5 and 10), then mean across draws:
    mc_predictions = inverse_transform_fun(mc_draws).sum(-1, keepdim=True).mean(0)
    # convert to a dataframe
    return TimeSeriesDataset.tensor_to_dataframe(
        mc_predictions,
        times=dataset.times(),
        group_names=dataset.group_names,
        measures=['predicted'],
        **kwargs
    )

[15]:

df_mv_pred = sum_mc_preds_as_df(
    forecast_mv,
    dataset_pm_mv,
    inverse_transform_fun=lambda x: 10 ** x,
    group_colname='station',
    time_colname='date'
)
df_mv_pred.head()

[15]:

	predicted	station	date
0	516.852661	Aotizhongxin	2013-03-01
1	175.849777	Aotizhongxin	2013-03-02
2	137.658920	Aotizhongxin	2013-03-03
3	133.654449	Aotizhongxin	2013-03-04
4	106.212036	Aotizhongxin	2013-03-05

Evaluating Performance¶

[16]:

def get_station_error(df: pd.DataFrame, pred_colname: str = 'mean', actual_colname: str = 'actual') -> pd.DataFrame:
    return (df
             .assign(sq_error=lambda df: (df[pred_colname] - df[actual_colname]) ** 2)
             .groupby(['station'])
             ['sq_error'].mean()
             .reset_index()
             .assign(rmse= lambda df: df['sq_error'] ** .5))

def agg_within_group_err(df: pd.DataFrame, error_col : str = 'rmse', group_col: str = 'station') -> pd.DataFrame:
    df = df.copy(deep=False)
    df['error_norm'] = df[error_col] - df.groupby(group_col)[error_col].transform('mean')
    return df.groupby('model').agg(**{error_col : (error_col, 'mean'), 'sem' : ('error_norm', 'sem')})

[17]:

df_fct_err = pd.concat([
            df_uv_pred
             .loc[lambda df: df['date'] > SPLIT_DT,:]
             .pipe(get_station_error)
             .assign(model='univariate')
            ,
            df_mv_pred
             .loc[lambda df: df['date'] > SPLIT_DT,:]
             .merge(df_aq.loc[:, ['station', 'date', 'PM']])
             .pipe(get_station_error, pred_colname='predicted', actual_colname='PM')
             .assign(model='multivariate')
]).reset_index(drop=True)
df_fct_err.sort_values('station').tail(6)

[17]:

	station	sq_error	rmse	model
21	Tiantan	22086.270448	148.614503	multivariate
9	Tiantan	23425.119141	153.052673	univariate
22	Wanliu	19955.333474	141.263348	multivariate
10	Wanliu	21000.425781	144.915237	univariate
11	Wanshouxigong	24935.359375	157.909332	univariate
23	Wanshouxigong	23582.429040	153.565716	multivariate

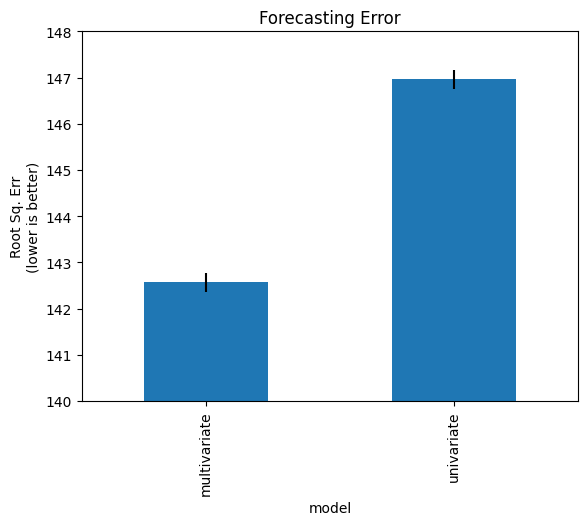
Below we aggregate the performance across stations (controlling for within-station variation to reduce noise).

We see the multivariate approach outperforms the univariate one despite the fact that we are just comparing univariate forecasts! That is, modeling the two types of PM with a multivariate approach was better for predicting their total than simply modeling that total directly.

[18]:

df_fct_err_agg = agg_within_group_err(df_fct_err)

# https://chris-said.io/2014/12/01/independent-t-tests-and-the-83-confidence-interval-a-useful-trick-for-eyeballing-your-data/
from scipy import stats
sem_multi = -stats.norm.ppf((1 - .83) / 2)

df_fct_err_agg['rmse'].plot(
    kind='bar',
    yerr=df_fct_err_agg['sem'] * sem_multi,
    ylabel="Root Sq. Err\n(lower is better)",
    title="Forecasting Error",
    ylim=(140,148)
)
plt.show()

../_images/examples_air_quality_27_0.png

Expanding Window Approach¶

One limitation to evaluating performance with a single train/val split-date is we run the risk that our results are sensitive to that particular split.

An alternative approach is an “expanding window”: we loop over the series, training on increasingly long sections, and forecasting on a fixed period beyond this. For short series, it might make sense to retrain on each iteration.

However for longer series, to speed up the process, we might want to simply use a particular date-range for training, then do our expanding window procedure on the held out remainder. (This is challenging in many forecasting APIs because they do not allow passing new series – or extensions of the trained series – at inference time, but instead require retraining.)

In torchcast, it’s easy to apply an expanding-window method with the n_step argument, avoiding the need for any refit -> forecast external loop.

[19]:

with torch.no_grad():
    one_mo_uv = kf_pm(
        dataset_pm.tensors[0],
        start_offsets=dataset_pm.start_datetimes,
        n_step=30
    )
    one_mo_mv = kf_pm_mv(
        dataset_pm_mv.tensors[0],
        start_offsets=dataset_pm_mv.start_datetimes,
        n_step=30
    )

df_backtest_err1mo = pd.concat([

    one_mo_uv
    .to_dataframe(dataset_pm, time_colname='date', group_colname='station', conf=None)
    .pipe(inverse_transform)
    .loc[lambda df: df['date'] > SPLIT_DT, :]
    .pipe(get_station_error)
    .assign(model='univariate')
    ,

    sum_mc_preds_as_df(one_mo_mv,
                          dataset_pm_mv,
                          inverse_transform_fun=lambda x: 10 ** x,
                          group_colname='station',
                          time_colname='date')
    .loc[lambda df: df['date'] > SPLIT_DT,:]
    .merge(df_aq[['station', 'date', 'PM']])
    .pipe(get_station_error, pred_colname='predicted', actual_colname='PM')
    .assign(model='multivariate')
])

df_backtest1mo_err_agg = agg_within_group_err(df_backtest_err1mo)

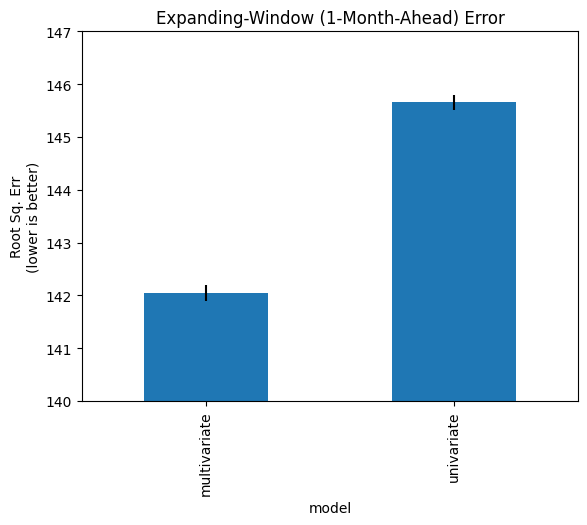
df_backtest1mo_err_agg['rmse'].plot(
    kind='bar',
    yerr=df_backtest1mo_err_agg['sem'],
    ylabel="Root Sq. Err\n(lower is better)",
    title="Expanding-Window (1-Month-Ahead) Error",
    ylim=(140,147)
)
plt.show()

../_images/examples_air_quality_29_0.png

Adding Predictors¶

In many settings we have external (a.k.a. exogenous) predictors we’d like to incorporate. Here we’ll use four predictors corresponding to weather conditions. Of course, in a forecasting context, we run into the problem of needing to fill in values for these predictors for future dates. For an arbitrary forecast horizon this can be a complex issue; for simplicity here we’ll focus on the 4-week-ahead predictions we used above, and simply lag our weather predictors by 4.

[20]:

from torchcast.process import LinearModel

# prepare external predictors:
predictors_raw = ['TEMP', 'PRES', 'DEWP']
predictors = [p.lower() + '_lag30' for p in predictors_raw]
# standardize:
predictor_means = df_aq.query("dataset=='train'")[predictors_raw].mean()
predictor_stds = df_aq.query("dataset=='train'")[predictors_raw].std()
df_aq[predictors] = (df_aq[predictors_raw] - predictor_means) / predictor_stds
# lag:
df_aq[predictors] = df_aq.groupby('station')[predictors].shift(30, fill_value=0)

# create dataset:
dataset_pm_lm = TimeSeriesDataset.from_dataframe(
    dataframe=df_aq,
    dt_unit='D',
    y_colnames=['PM10_log10','PM2p5_log10'],
    X_colnames=predictors,
    group_colname='station',
    time_colname='date',
)
dataset_pm_lm_train, _ = dataset_pm_lm.train_val_split(dt=SPLIT_DT)
dataset_pm_lm_train

[20]:

TimeSeriesDataset(sizes=[torch.Size([12, 1088, 2]), torch.Size([12, 1088, 3])], measures=(('PM10_log10', 'PM2p5_log10'), ('temp_lag30', 'pres_lag30', 'dewp_lag30')))

[21]:

_processes = []
for m in dataset_pm_lm.measures[0]:
    _processes.extend([
        LocalTrend(id=f'{m}_trend', measure=m),

        Season(
            id=f'{m}_day_in_year',
            period=365.25,
            dt_unit='D',
            K=4,
            measure=m,
            fixed=True
        ),

        Season(
            id=f'{m}_day_in_week',
            period=7,
            dt_unit='D',
            K=2,
            measure=m,
            fixed=True
        ),


        LinearModel(
            id=f'{m}_lm',
            predictors=predictors,
            measure=m
        )
    ])
kf_pm_lm = KalmanFilter(
    measures=dataset_pm_lm.measures[0], processes=_processes
)

[22]:

# fit:
y, X = dataset_pm_lm_train.tensors
kf_pm_lm.fit(
    y,
    X=X, # if you want to supply different predictors to different processes, you can use `{process_name}__X`
    start_offsets=dataset_pm_lm_train.start_datetimes,
    n_step=5,
    every_step=False
)

Initializing PM10_log10_trend.position to 1.9197293519973755
Initializing PM2p5_log10_trend.position to 1.7517921924591064

[22]:

KalmanFilter(processes=[LocalTrend(id='PM10_log10_trend'), Season(id='PM10_log10_day_in_year'), Season(id='PM10_log10_day_in_week'), LinearModel(id='PM10_log10_lm'), LocalTrend(id='PM2p5_log10_trend'), Season(id='PM2p5_log10_day_in_year'), Season(id='PM2p5_log10_day_in_week'), LinearModel(id='PM2p5_log10_lm')], measures=['PM10_log10', 'PM2p5_log10'])

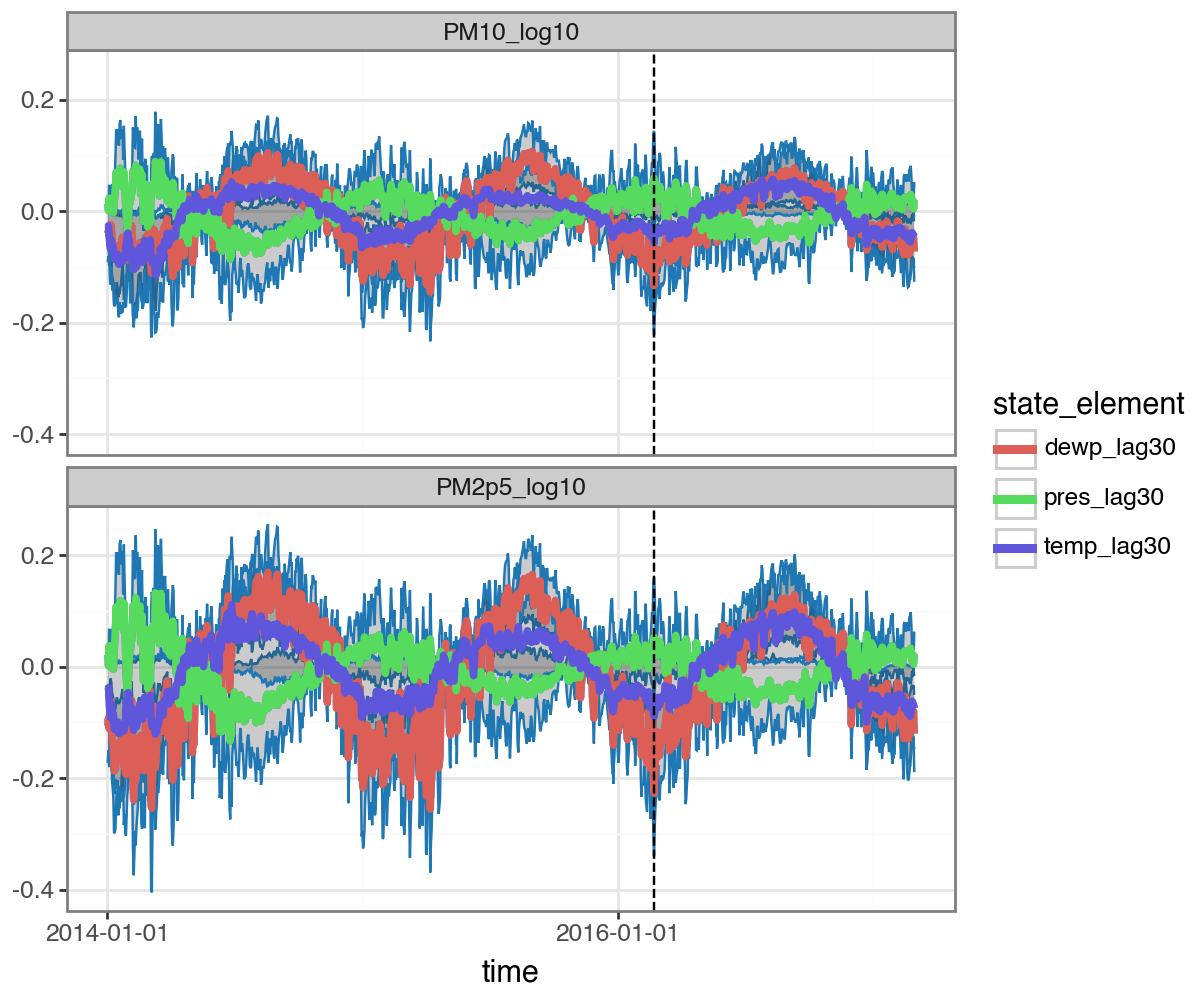
Here we show how to inspect the influence of each predictor:

[23]:

# inspect components:
with torch.no_grad():
    y, X = dataset_pm_lm.tensors
    one_mo_lm = kf_pm_lm(
        y,
        X=X,
        start_offsets=dataset_pm_lm.start_datetimes,
        n_step=30
    )
one_mo_lm.plot(
    one_mo_lm
    .to_dataframe(dataset_pm_lm, type='components')
    .query("process.str.contains('lm')")
    .query("time > '2014-01-01'"),
    split_dt=SPLIT_DT,
    figure_size=(6,5)
) + facet_wrap('measure', ncol=1)

Subsetting to groups: ['Changping']

../_images/examples_air_quality_35_1.png

Re-Evaluate Performance¶

Now let’s look at the change in error from our earlier multivariate model vs. one that includes predictors.

We can’t compare the forecasts, since we have a fixed lag on our predictors. But we can easily compare the expanding-window results:

[24]:

df_backtest1mo_err_agg2 = agg_within_group_err(
    pd.concat([
        # old ones:
        df_backtest_err1mo,
        # new one:
        sum_mc_preds_as_df(one_mo_lm,
                              dataset_pm_lm,
                              inverse_transform_fun=lambda x: 10 ** x,
                              group_colname='station',
                              time_colname='date')
        .loc[lambda df: df['date'] > SPLIT_DT,:]
        .merge(df_aq[['station', 'date', 'PM']])
        .pipe(get_station_error, pred_colname='predicted', actual_colname='PM')
        .assign(model='mv_with_preds')
    ])
)

df_backtest1mo_err_agg2['rmse'].plot(
    kind='bar',
    yerr=df_backtest1mo_err_agg2['sem'] * sem_multi,
    ylabel="Root Sq. Err\n(lower is better)",
    title="Backtesting (1-Month-Ahead) Error",
    ylim=(140,147)
)
plt.show()

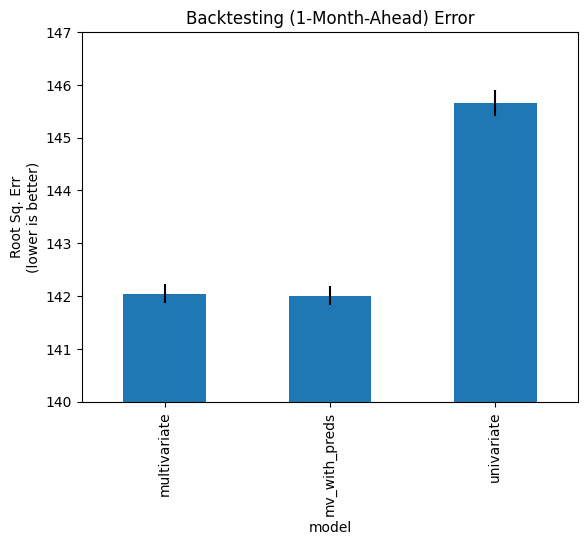
../_images/examples_air_quality_38_0.png

We see that the lagged predictors do not significantly impact performance.